A couple of years ago, John Sansom wrote a blog post comparing the performance of two different ways to get the maximum value from a column: MAX() and TOP (1).

In the conclusion, he states:

When a clustered index is present on the table and column that is to be selected, both the MAX() operator and the query (SELECT TOP 1 ColumnName order by ColumnName) have almost identical performance.

When there is no clustered index on the table and column to be queried, the MAX() operator offers the better performance.

Now for this specific case, that is quite true. But I find it alarming when people take his conclusion and believe it applies to every single scenario – so much so that they make policy decisions around prohibiting the use of TOP 1 in all situations (regardless of whether the ordering is on an indexed column, a non-indexed column, or even an aggregate). This isn't John's fault, of course. It's just the nature of people who believe that something they see once means it applies everywhere (SELECT without ORDER BY, anyone?).

Recently a user asked the community to help them re-write a query that was currently using TOP 1 – not because the query was slow or produced the wrong results, but because they were told they could no longer use TOP 1. When asked why, they simply pointed at John's blog post above, and were going with the theory that TOP 1 is always slower and it must be eradicated from their codebase.

Not being a big fan of generalizations, I tried to explain that John's situation was not quite the same – for one he was getting the max value from a single column, whereas the query in question actually wanted the max from an aggregate in a subquery – but they didn't seem to want to have anything to do with it. So, naturally, I set out to run some tests myself. Here is the query that was subject to refactoring – essentially they wanted the team name with the highest number of members:

SELECT t.name
FROM   team AS t
INNER JOIN (SELECT TOP 1 COUNT(*) AS membercount,
                          teamID
                   FROM   dbo.teammember
                   GROUP BY teamID
                   ORDER BY COUNT(*) DESC) AS team_with_most_members
         ON t.id = team_with_most_members.teamID;

Two other solutions were offered (well, three, but one didn't work). One was from me:

SELECT t.name FROM
(
    SELECT
        TeamID,
        rn = ROW_NUMBER() OVER (ORDER BY c DESC)
    FROM
    (
        SELECT
            TeamID,
            c = COUNT(*)
        FROM dbo.TeamMember GROUP BY TeamID
    ) AS x
) AS y
INNER JOIN dbo.Team AS t
ON y.TeamID = t.ID
WHERE y.rn = 1;

And one was from Wil:

 SELECT t.name FROM team AS t 
JOIN teammember AS tm ON tm.teamID = t.ID 
GROUP BY t.Name
HAVING COUNT(tm.id) = (SELECT MAX(members)
 FROM (SELECT COUNT(id) members FROM teammember GROUP BY teamid) AS sub)

To compare the three options, I first created some sample tables. The first was the main Team table:

CREATE TABLE dbo.Team
( 
  ID   int PRIMARY KEY CLUSTERED, 
  Name VARCHAR(32)
);

Then I created two versions of the TeamMember table, one with a clustered index on the TeamID column, and one with a non-clustered index:

CREATE TABLE dbo.TeamMember_A
(
  ID     int IDENTITY(1,1) PRIMARY KEY NONCLUSTERED,
  TeamID int, 
  Name   varchar(32)
);
 
CREATE CLUSTERED INDEX x ON dbo.TeamMember_A(TeamID);
 
CREATE TABLE dbo.TeamMember_B
(
  ID     int IDENTITY(1,1) PRIMARY KEY CLUSTERED,
  TeamID int, 
  Name   varchar(32)
);
 
CREATE INDEX x ON dbo.TeamMember_B(TeamID);

To populate them with a reasonable volume of data, I performed some creative queries against sys.objects. First I populated a table variable with a group of random rows based on object_id, with the first column being the TeamID, and the second column being the number of rows that I would insert into the TeamMember tables:

DECLARE @src TABLE
(
    TeamID int, TeamSize int
);
 
;WITH SampleData(TeamID, TeamSize) AS
(
    SELECT [object_id] % 10000,
           CONVERT(int, [object_id] / 15000.0) + 1
    FROM sys.objects
)
INSERT @src(TeamID, TeamSize) 
  SELECT TOP (30) TeamnID, TeamSize
  FROM SampleData
  WHERE TeamSize > 0
  ORDER BY TeamSize DESC;

This created 30 values like this (the last several rows yield c = 1):

Now that I had a set of 30 teams to create, I could use a cursor and a while loop (fun, fun) to populate the TeamMember tables. Could I have used a numbers table and done a cross join or something to avoid the loop? Sure, but this was easy enough and it is not exactly production code.

DECLARE @TeamID int, @TeamSize int, @i int;
 
DECLARE @c cursor READ_ONLY
  FOR SELECT TeamID, TeamSize FROM @src;
 
OPEN @c;
 
FETCH NEXT FROM @c INTO @TeamID, @TeamSize;
 
WHILE @@FETCH_STATUS <> -1
BEGIN
    SET @i = 1;
 
    WHILE @i <= @TeamSize
    BEGIN
        INSERT dbo.TeamMember_A(TeamID, Name)
            SELECT @TeamID, CONVERT(varchar(32), @TeamID);
 
        INSERT dbo.TeamMember_B(TeamID, Name)
            SELECT @TeamID, CONVERT(varchar(32), @TeamID);
 
        SET @i += 1;
    END
 
    FETCH NEXT FROM c INTO @TeamID, @TeamSize;
END
 
CLOSE c;
DEALLOCATE c;

A quick count showed we had 30 rows in the Team table, and about 1.3 million rows in the TeamMember tables (with individual teams ranging from one row to 140,000 rows).

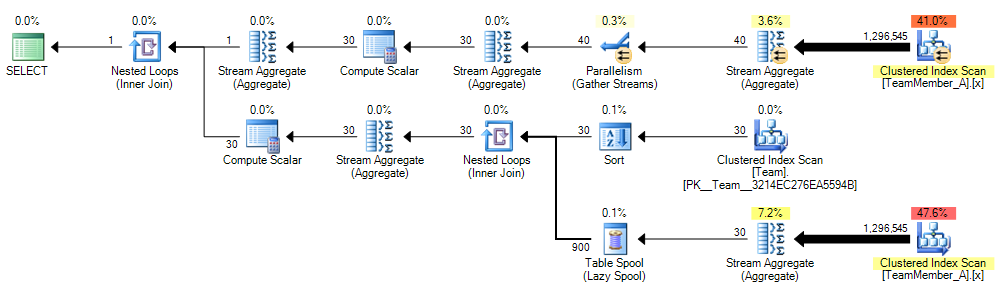
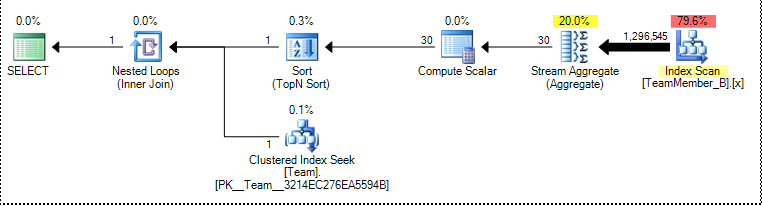
Now we could put our three queries to the test! I opened up my trusty copy of SentryOne Plan Explorer and pasted the three queries into the Command Text pane. I clicked the "Actual Plan" button, which goes to the server, runs the query, retrieves the actual plan, and discards the results. First I ran it for the A table (clustered index on TeamID), and these were the results from the Statements Tree tab:

Similar results for the B table (the one with just a non-clustered index on the TeamID column):

In both cases, Wil's solution came out at about twice the cost as the original query (and my proposed replacement). You can see where the doubling comes in from Wil's graphical plan (an extra scan), compared to the other two (the screen shots are presented in the same order as the 6 rows shown in the Statements Tree rows above – click on any to enlarge):

TeamMember_A

Original

Aaron

Wil

TeamMember_B

Original

Aaron

Wil

I tried running the tests again with parallelism off, and while the plans looked a little different, the overall results were nearly identical (~50/25/25 split).

Conclusion

Generalizations are dangerous. Even if a situation looks similar to the one you've got, you owe it to yourself to test. Especially in a case where you've been asked to change your code to improve performance, and you've actually accepted a solution that performs worse.