Most of the recent – what I'll call – "discussions" about content aggregators have revolved around content theft. I'm not going to flip-flop on that topic: when you use someone else's work, you ask first, and if given the okay, you cite it. You can't take my blog article and post it on your site, implying that it is your own. Likewise, you shouldn't be taking a Books Online topic, changing three words and adding an intro sentence, and making that a blog post. I think this stuff is pretty clear-cut; you either get permission to reproduce content, or you summarize and provide a link. Nobody likes it when you take credit for their work, but hardly anyone is going to complain if you drive traffic to them (even if you have partly benefited by driving traffic to your site first).
On the plus side, while I feel pretty strongly about it, I haven't really been a victim of this (yet). Either the content thieves of the SQL Server world have not yet discovered me, or they know who I am and don't think my work is worthy of stealing. No skin off my back either way.
This is NOT about content theft
What I have discovered lately is a little more benign than outright theft, but certainly less cool than simple traffic building. In most cases I am leery of mentioning a vendor by name, but in this case I am simply not afraid of stating who it is: sswug.org. I'm not going to link you there because right now I don't believe they deserve the traffic.
So what is my beef?
A little over a week ago ,in my morning e-mail from sswug, I saw the following:

Notice how they have sections for featured articles, full-member (e.g. PAID) articles, and free resources. Also notice how an article I wrote is featured under the "Full-Member Articles" section. To me, this implies that you must be a paid member in order to read the article. (If you don't see it this way, I'd love to hear about how your perception differs, and why.) So just to see whether they had stolen my content to sell, or simply linked to it, I clicked on the link. That led me to the first couple of sentences of my article in a summary, hosted on sswug.org's site, surrounded by ads.

Clicking on the "Read Article" link, I am greeted with yet another page hosted on sswug.org's site, again surrounded by ads, this time with a button encouraging me to pay for a full membership to the site (which doesn't even host the article they're talking about):
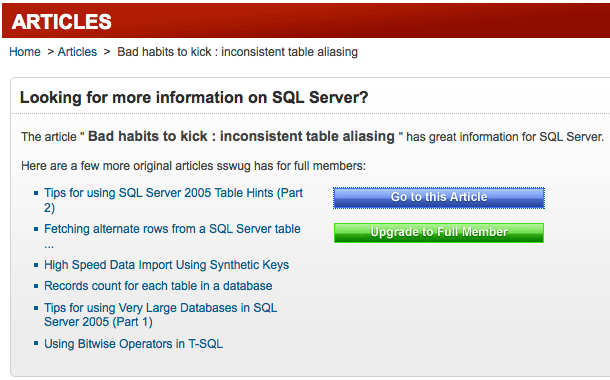
If you take the blue pill, you will go to my article, and that's the end of it. However, if you take the green pill, you will be asked for your credit card, and might still be under the assumption that this is the only way you can read my mediocre "bad habits" article. Even the wording is misleading: "here are a few more original articles sswug has for full members:" – implying that the article in question is an original sswug article, and is only available to full members.
Now, notice the different behavior you get with one of the other "Full-Member Articles" listed in the same section as mine. When you click on the link for "High Speed Data Import Using Synthetic Keys," you get a similar summary with a "Read Article" link, but when you click on that link, you get this:

Which means in this case you really DO need to become a full member to read the article. So why was my article listed in the same category? I think that they benefit from mixing the two article types in two different ways: (1) if the user hits an original article, they know they have to upgrade, but could also assume that is true also for the articles they didn't yet hit; and, (2) if the user hits an article that is free and hosted externally, the messaging around the obstacle course they have to take there, could mislead them into believing that it is NOT a free article and that they need to become a full member to see it. I wonder how many people are duped in either of these ways?
I'm sorry if anyone feels differently, but I think this is a deplorable way to make money. Trick someone into paying for content that you know full well is available for free elsewhere, by mixing linked articles you collected from RSS with the few bona fide articles you've actually paid for. In some circles this is called bait & switch; in others it has a worse name. Shame on you, Mr. Swynk.


Thanks Chris. Their challenge, of course, is that on an average day they don't have new, exclusive content to offer, so if their categories were more clear, the "paid members-only content" section would look like Mrs. Hubbard's cupboard more often than not. At least in the sampling of newsletters I took, going back about 6-8 months.
Agreed Aaron.
I'm a free sswug member and I've been confronted with that upgrade screen many dozens of times.
I assumed from these experiences that all items I was likely to be interested in at sswug were only available for paying members …so I stopped reading the sswug newsletter.
Not only is sswug annoying you (and possibly misleading folk into signing up for a paid subscription) but they are also shooting themselves in the foot …my guess is that a fair percentage of the free folk simply walk away in annoyance just like me. If sswug's "aggregation" items were more clearly (?? fairly) labelled, sswug might have a better chance of switching some of the free folk over to paid membership.
I completely agree with you on this, Aaron, and would also like to thank you for bringing it up. Like Kevin, I will be awaiting Stephen's action on this to see how he resolves the issue. I know the greater SQL Server community will be watching as well and hope the actions help continue to further the impressions of all in the technical world of the SQL Server community as being a highly ethical, collaborative, and community focused group.
Hi guys,
Sorry I'm late to the party. I was on a no-laptop vacation last week.
Before I weigh in, I must declare that I have been in the past and am currently a paid SSWUG vConf speaker. I'm not sure how strongly that colors my opinion, but you should know about the potential conflict of interest before I give voice to my thoughts.
I see two main questions and look at this from a few different perspectives. The main questions are "Is it ok to aggregate?" and "What is the proper method of attribution when aggregating external content?" The short answers to these are "Yes" and "With unambiguous credit given to the original author(s)". SSWUG is doing the first part well and the second part very poorly.
I have a couple perspectives in mind when I consider this situation:
AS A CONSUMER: A lot of people have used strong words to characterize the way that SSWUG has represented its external links. My first thought is "Easy there big fella". I -wish- I had somebody to do that for me. My Google Reader account is constantly at 1000+ unread, and that's AFTER a few hours of reading while on the couch with my kids watching a TV show. I really WANT someone to filter all of the MSSQL content out there and point out what's really good. Although I don't pay for a SSWUG membership or read the newsletters, I'd be willing to pay for it if I knew that I'd get pointers to the cream of the crop amongst all the MSSQL content out there. While the aggregation approach seems to be widely reviled based on the feedback here, I think it is good thing, assuming it is done right. Doing "it" right is the core question here. More on that in the next section. (As an aside, I like Steve Jones' Database Weekly e-newsletter from SQLServerCentral.com as my main aggregation of MSSQL news and content. He does attribution of content very well and the content is always good.)
AS A WRITER/BLOGGER: As Aaron points out, how you present content created by another person is paramount. I have no problem with anyone reposting my free content (blog posts, YouTube videos, etc) as long as I'm given proper attribution. If it's commercial content such as one of my books, then it had better follow the legal hurdles accordingly (no BitTorrents, please) or I will "drink your milkshake", to use the phrase. Again, as Aaron points out, SSWUG seems to have veered into shady territory. External content must be represented as such and "full-member content" should indicate content available only to full, paying members of SSWUG. Any ambiguity, if intentional, is a breach of ethics.
AS AN ETHICAL PERSON: I've known Steve for a while now and think highly of him. I can't imagine that he's doing this to knowingly take advantage of a gray area. As Steve mentions, he's been doing this for years. Sometimes, when you do the same thing day after day, it becomes someone invisible and doesn't register on a conscious level. I'm the kind of guy who gives the benefit of the doubt, who assumes good intentions unless proven otherwise. (Not always the wisest position, I know. I've been burned before.) We all make mistakes. Heck, I once plagiarized a poem in 10th grade English and I still feel terrible about it. But sometimes they're a little under our level of mindfulness and just slip through the cracks – like the way I flog Hertz cars like a rented mule. ;^)
I think that you, Aaron, have done a big service to the wider community by bringing this to light. The proof is in the pudding, so to speak, based on how Steve responds. Will he do what is clearly the right thing and put obvious delineations between external and internal content in future newsletters and on-site?
I'm encouraged that Steve will, based on his quick and forthright response. Let's see what happens next…
-Kev
Glenn Berry: Slide the slider thingy on the right all the way to the top and start reading from there down.
I'm an accidental DBA, just trying to keep my SQL servers running, and have used many sites including SSWUG. I receive his daily newsletter and I have to agree with Arron Bertrand, it can be confusing which content is for free and which is for paid members. It makes me think it's something special if the content is listed and I have to sign in for it. Especially when the content is freely available elsewhere. If you don't want SSWUG to use your content then that should be the end of it.
Hi Glenn,
There are other differences between Google Reader and SSWUG that you are ignoring.
If you don't think I should have the final say on where and how content I own is distributed, that's your call. I've said my piece.
:{> Andy
Glenn, it appears that you missed the point of both my original post and my reply to your comment. As per:
"What about linking? If I link to a good blog post from Aaron in my blog, should I ask his permission first? What about retweeting?"
That depends. Did you entitle your blog post or tweet, "Here is some good information, but you'll have to pay to see it."?
For the third time, I am not upset with SSWUG because they linked to my content. I am upset with them because they linked to my content under the guise that the reader would have to pay before they could see the content. Stephen quickly adjusted the wording of the headline without much fuss, so he must have seen what I was getting at (and what handfuls of people here have agreed with).
I'm not sure which part of this you're not understanding, but you're drawing on examples that have nothing to do with what I'm complaining about.
Hi Andy,
I'm not here to defend SSWUG or the way they run their web site. I can see where people would not like how memberships are being sold. I was simply trying to make a point about aggregation and linking in general.
Anyone who has a blog or web site will find their content aggregated by Google Reader, pretty much whether they like it or not. Google is certainly benefitting at least indirectly from all of the content that they are aggregating. Is that unethical?
What about linking? If I link to a good blog post from Aaron in my blog, should I ask his permission first? What about retweeting? Should I ask permission before I retweet someone? What about Search engines? Google makes billions off of advertising driven by their search results.
It just seems that we could be on a slippery slope, where people would be less able to find good information if every content provider demands permission for simply linking to their content.
This was one of the first things I saw many years ago when I first stumbled across the SSWUG site. I signed up for the newsletter, the trial membership, then noticed that most of the links for paying members took me to other sites. I resolved then that I would never pay for a membership to SSWUG. I've mentioned this in surveys that SSWUG has sent out, but apparently I was a minority there. I also skim the content, but tend to skip over anything listed for members only just because it's not clear that the link is external and free.
Stephen, you've responded already that you're aggregating content and that people don't need to pay for external links, but it would be great if you put in a new section in your e-mail newsletter to show those links as free and external. It would be even better if you just redirected people through your site to those links without a need to log in and click through pages to get there, but that's your call. I appreciate that you want to help the community and that you sponsor and run online training events. However, I think that a couple changes to the newsletter format would go a long way to making it feel like the community's voice is being heard. 🙂
"whatDoIKnow", why would I sue them? I'm not trying to get any money out of them. I'm trying to help prevent others from getting duped into spending money for the wrong reason, that's all. Since Stephen has already changed the misleading heading on his daily newsletters from "Full-Member Articles" to "Latest Resources", then I consider it a win, and I'm glad I spoke out.
seems like this is bigger than what it is. i for one know why technie people make less than financial ppl cause we are so concerned with 'ethics' and open source 🙂 hmmmm, get over it, sue them or just leave them alone to try and make a dollar in this good ol' US economy.
Aaron,
Excellent catch – one that Mr. Wynkoop is obviously keeping an eye on as indicated in his response in the link provided above by Feodor where he defends his lack of response as "lost" email. Good job for calling him out on the carpet – it is the very reason I stopped going to his site. I'm sure he hopes that this will blow over, but hopefully others will chime in and see if we can take a little wind out of his sails. Maybe then articles that are available for free elsewhere will not be used to dupe people into subscribing to his site. Maybe if those handing out awards knew what was going on under the covers, the trophy case at SSWUGG would start collecting dust in all those empty spots. The guantlet I have to go through to actually get to a free article on SSWUGG insults my intelligence – I'm sure there are others who feel the same.
Aaron,
I was too hard on him at the end of my last comment. I've swapped emails and tweets with him in the past on the topic. At best I find the practice misleading, at worst, unethical. Almost every MVP I know donates their time and talent to the SQL Server community free of charge. And, almost every MVP I know has bills to pay and job that they do to pay them.
I believe it's up to every person – MVP or no – to decide where they draw the line between business and community activites. When is someone being unethical? I defer to the Supreme Court's definition of pornography: "I know it when I see it."
What bugs me about this is the deception. You were absolutely correct in your earlier point about the External Link icon. You didn't see it. The truth is: No one sees it and that is by design. It's visual deception. The human interaction with the web searches for links to click, and they are blue and underlined. So if Mr. Wynkoop wants to serve the community by aggregating free content (which he will argue you and I are "giving away anyway"), then do so by including in the same blue underlined link text as the external link the verbiage "(FREE EXTERNAL LINK)".
That'll happen.
If I wanted people to have to pay for my content – and I own my content, and so do you, even if we set the viewing price at $0.00 USD – I would raise the price.
I do not want people tricked into paying for my content. I do not want my content linked or associated with a site that participates in deceptive business practices for the sake of pue profit, regardless of the spin.
I responded to Glenn Berry's comment because I *have* complained to Mr. Wynkoop privately in the past. I believe he did remove the links to the post in question, but has continued to use my name and my posts and my thoughts and my material to generate profit for himself without any approval or so much as an email requesting permission. Add to that the fact that he is profiting from this continued deception, and it crosses the line, in my opinion.
Andy
Thanks Andy,
And just to be clear, I don't (and won't ever) want a cut of Stephen's revenue. Even if I were blogging for the money (which I'm not; trust me), I don't think it's honest money. To be perfectly frank, I think Stephen should offer a refund to any of his subscribers who feel they were duped into purchasing a subscription that they ultimately did not need. But who am I to say so? That's just what I would do, were I in his shoes.
A
Hi Glenn,
A lot of people have complained about SSWUG's practices – in private – and yet it continues.
This is really easy to fix: If anyone signs up after clicking the green button sign-up link from the third image above, work out a business arrangement with Aaron to compensate him for his contribution to your income.
This is point – Aaron is not being compensated for his original material linked to without his consent.
"Opt out" options – after discovery by the author whose material has been linked without permission/compensation, mind you, is not much of an option.
This has class action written all over it. Stephen, this is unethical. You should stop.
:{> Andy
Aaron, I though you might want to know that your blog post is mentioned here: http://feodorgeorgiev.com/blog/2010/03/and-best-things-are-almost-free/
Thanks!
Feodor
Aaron, I agree with you.
Glenn, obviously I am not complaining about aggregating feeds of other authors – you make it sound like I'm complaining about something that a LOT of sites out there are doing, which is simply not true. What I am raising a beef about is aggregating feeds that are freely available, and misrepresenting them as original SSWUG articles that you have to pay for. Whether that misrepresentation was intentional or not is another issue… the fact is that people could easily have been swayed to purchase a membership when they didn't have to, and there is no easy way to know how many people have done so.
Sure, I could have handled it differently. I could have had a personal conversation with Stephen, he could have committed to fixing the problem, and maybe the issue would have stopped happening in a week or in a month. However, I have sent personal e-mails to Stephen before (different issues), and they have gone without response. So who knows how seriously he would take the input of one person, vs. the input that has been gathered here. In the meantime, people could continue to be duped into buying that membership. With any luck, I've saved at least one person from doing so. I'm not trying to stop people from buying SSWUG memberships; I'm sure the exclusive content is useful and valuable to a lot of people. I just don't like the idea of tricking people into buying it for the wrong reasons. Since the public was being mislead for a long time, I think it is more appropriate to give Stephen a chance to respond here publicly, which he did gracefully.
I want to make it clear that I am only speaking for myself, not on the behalf of my employer. I think there is a big difference between republishing someone else's work with no attribution, passing it off as your own (which is plagarism and theft), and other things like linking and/or aggregating content (that is fully attributed).
Obviously, the first is illegal and morally wrong, while there are many grey areas in the second. RSS Agregators like Google Reader, Bloglines and NewsGator download millions of RSS feeds, store the content in their data centers, and make it available to their users.
Most people see this as a service that they appreciate, but some bloggers and web sites do not like this. Most web sites and bloggers like the extra exposure they get from aggregation, but sometimes resent the lost advertising revenue they may lose from direct visits to their site. Aggregators usually either directly or indirectly benefit from the content that they aggregate. It is not customary to ask the original author's permission to aggregate his feed, it is just automatically done when an end-user subscribes to the feed. If an original author objects, their feed can be placed on a "blacklist" so that it is no longer aggregated.
As far as linking to other people's content, I don't see any problem with that whatsoever. I don't even think I have to ask permission to link to someone else's content. Most people appreciate links, since it gives them more exposure. If someone I link to tells me to stop doing it, I would immediately comply. Personally, I have no problem with anyone linking to my content.
Generally speaking, I think it is better to try to resolve disputes privately before going public with them. I have no idea whether Aaron reached out to SSWUG before he blogged about this or not. I like and respect Aaron, but perhaps this could have been handled differently?
Your link should not have appeared under the heading Full-Member Articles. That's wrong. It should have appeared under Guest/Open Resources, which in itself should probably be reworded to Guest/Free Resources. Any links appearing there should be immediately accessible.
Years ago I discovered SSWUG republished for their paying members DBAzine.com articles I wrote. When I became a DBAzine author, I relinquished all rights to content they paid me for. DBAzine made a business agreement with SSWUG, so I had no basis for an objection.
"deceptive" isn't a strong enough word for what they're doing
"Scum Sucking Worthless Usurping Goats" comes closer
Aaron,
Thank you much for a very detailed explanation.
It would be interesting to hear Kevin's and Paul's opinion.
Yes Stephen, I understand that they eventually get to the article for free. That's not my beef. Let me explain again why I think this is worthy of discussion, because you still seem to think it isn't "a big issue."
My concern is that they are, from the very outset, led to believe that these "free and external" links are in fact only accessible by one who is a "Full-Member." That's exactly what the headline has told them.
Then getting to the article is not a mere click away. Oh no. They have to click the link in the e-mail, then login (or re-register/remind password if they can't), then click on the link to the summary page, then finally click on the button that says, "Take me to the article" – if they don't inadvertently or intentionally click on the very close-by button, "Upgrade to Full Member." It is clear that along this path, you are led to believe that the article is eligible only to full members. If you don't see this, then I will concede to your earlier point – you have been staring at this too long to see the problem.
All the while blasted with advertising all over the place, and several further prompts to sign up for a paid membership. Which I'm sure some do, if they already have it in their head (due to the poorly-worded headline) that, in order to read the article in question, they need to pay first.
Did I mention that they can access these external links for free? There is no paid membership required.
…and yes, we're updating the heading to be more clear. Sorry if I wasn't clear on that above.
In a newsletter from February 25th, there was a link to Merrill's article on view myths featured in the "Full-Member Articles" section:
http://sqlblog.com/blogs/merrill_aldrich/archive/2010/02/11/busting-a-persistent-myth-views-are-executed-before-enclosing-queries.aspx
In the January 11th newsletter, there was a link in that same section to Linchi's article on using hostnames to connect to SQL Server:
http://sqlblog.com/blogs/linchi_shea/archive/2009/12/28/bad-database-practices-allowing-apps-to-connect-to-the-hostname.aspx
On September 29th there was a link to K Brian Kelley's article on dynamic SQL and ownership chaining, also purported to be a "Full-Member Article":
http://www.mssqltips.com/tip.asp?tip=1822
On June 30th, there was a similarly featured "Full-Member Article" linking out to Yan Pan's Change Tracking article on Database Journal:
http://www.databasejournal.com/features/mssql/article.php/3824196/Introducing-Change-Tracking-in-SQL-Server-2008.htm
So clearly – and I'm glad you asked the question – this is not an entirely new "feature" that is being exploited. That was just a very random sampling; I paged through my SSWUG folder and grabbed the message on the bottom list of each page, and tried a random link from each one. I can cite several more examples and provide screen shots, if you think this is being constructed somehow to appease you. The nice thing about the SSWUG newsletter is that the format (and obviously the content practices) haven't changed in months, so it's very easy to spot check the messages still in your inbox somewhere. 🙂
Now, the sad part is, we'll never know how many people spent good money on a membership to the site, not knowing that they could have read the article for free and without ever having heard of SSWUG. 🙁
Alex, I did not go back and look at my archive, but I do plan to take a random spot check on the ones I've kept over time. This was just the first time I noticed because it was my article that seemed to be pushed as exclusive SSWUG content, which of course I knew it was not.
Aaron,
Is putting a link to free content in paid subscription area is a new practice on that site, or is it something that has been happening for a long time?
I agree with you as well Aaron. A slight redesign could easily make everyone happy, and it's too bad that doesn't seem to be in the cards. Is there a published way to opt out?
And Alex, as another aside, in today's e-mail newsletter there are four links under "Full-Member Articles" – and all four link to, surprise surprise, external content neither hosted nor paid for by SSWUG. Do you still think this is not misleading, that there is another side to hear, and that there is any reason to condone this behavior? It looks like SSWUG puts out about 2 original articles a week, but their daily newsletter would look pretty empty if those were the only links included. So I guess this is their way to make their "Full-Member Articles" section seem more substantial, and further dupe people into believing there is a ton of unique and interesting content available only to paid members. When in fact most of this content (at least links; not talking about videos and VCs which are represented elsewhere) is freely available to anyone with an Internet connection.
Alex, I am more than open to hearing both sides. That is why I posted. Clearly I have an opinion but anyone who has an opposing view is more than welcome to comment here. If I didn't state my opinion by creating this blog post, then where would we be having such a debate? So how do I further act on your suggestion to hear both sides?
(As for isolated, note that there is more than one free link in the paid subscription area of the e-mail I referenced above. I have not gone back and checked other newsletters but it would be a trivial thing for anyone to follow up on.)
Aaron,
I am sorry if my post was not clear. My only suggestion is "to hear both sides in this dispute". I must admit that I stopped subscribing to and have not read sswug newslettter in at least two years, but I thought that most likely one of two alternatives happened:
1. Putting your link in paid subscription area is an isolated mistake, then let us give the person the benefit of doubt.
2. Putting a link to free content in paid subscription area is common practice on that site. If that is the case, than you should not be the first to notice. Surely at least some have noticed it before and have their opinions. Maybe someone thinks that's OK and have their reasons? Let us hear alternative opinions.
No deception intended at all, as I mentioned in my email response.
We will update the heading to be more clear.
As I mentioned, it's important to understand; external links are free – registration only – like 99% of sites out there.
I love working with the SQL community at large and providing great resources. I work hard to provide good services, to work with all sorts of people for presentations, articles and such. If that is mis-perceived or not clear or … whatever, from time-to-time, it's on me. Some of these pages I've been staring at for so many years that I see what I want to see, not how someone else may read a heading or whatever.
There's not a bit of malice or whatever in what we do, what I do.
PS – your materials were removed, of course. I just didn't want to leave this hanging.
Stephen, hats off for responding promptly and directly.
You're talking about the second image, when you reference the globe (which I didn't notice at all, by the way). Did you skip over the first one? Where a link to my free blog post is listed under "Full-Member Articles"? Do you not see how this is misleading? While virtually nobody will go and read your terms of service word for word anyway, it certainly does not say anything in there about "misplacing" free external links under headlines that imply that the content is neither free nor external. I hope you don't think I'm making something out of nothing here; this is pretty serious deception, and if you don't see that, then quite frankly I have no choice but to believe you are being intentionally obtuse (I know that this is not an intelligence or comprehension problem).
I will repeat my request once again: please stop linking to any of my content from your newsletters and web sites; even the links you might have decided to categorize correctly and less selfishly.
I like publicity as much as the next guy, but I have the right to refuse allowing others to profit from my work in a dishonest way.
(from email also sent)
We're not looking to deceive anyone at all. In fact, external links are free – no membership required at all (registration, yes. Membership/any payment, no). In addition, all external links are noted with the "globe" icon next to the title of the post/article/resource, as you showed in your blog post image. Further, in our terms of service (http://www.sswug.org/tos.aspx), this is outlined and explained:
CONTENT AGGREGATOR AND ORIGINAL CONTENT
SSWUG is both an aggregator, promoting articles on other sites, and an author of original author content. A good part of the service we offer is to pull together links to articles, internal and external to SSWUG.ORG and present them to members and guests as appropriate. In this area, we are basically a "private," focused search engine. If you are seeing referrals from SSWUG and our readers, that's because we're promoting your articles. We do not re-publish your articles, we only take a one- or two- sentence summary and then link directly to the article on your site. Articles that are not based at SSWUG.ORG will be denoted with a symbol on the "headline details" page or similar. |globe symbol shown|
We do explain this numerous times on the site and try to make people aware of it, but clearly it can be missed.
Still, since no payment or full membership is required at all to visit external links, I wouldn't imagine this is a big issue.
We have full-time staff responsible for finding great content and letting our readership know about it. It's not automated, it's people. That, combined with other things we offer like the weekly show, webcasts, and a LOT of content that's both free and members-only – I don't think it's unreasonable to ask people to register on the site.
We work very hard to bring great content to our user base and are proud of being able to offer both the free and paid services. Our readership really likes having a single starting point for articles, resources, video programs, conferences, virtual conferences, workshops and other learning tools, whether they're on the site or off the site. We promote external sites (like your posts, for example) and hope that it results in good traffic to your site and the sites of others we let readership know about.
I hope this helps – let me know if not. I'm happy to remove links to your work if you'd still like me to. I wanted to explain though; it's free access. Just click the button and people are on their way.
Alex, I never said SSWUG is horrible and nobody should do anything with them. I have pointed out a very clear and obvious case of them abusing other peoples' work for profit. I have also sent a personal e-mail directly to Stephen Wynkoop, asking him to (a) stop doing so, at the very least with my content, and (b) publicly respond here, if he so desires. Let's say that Paul, Kevin, Glenn, and the MVP leads were among the many people that clearly weren't aware that this bait & switch was going on (because not saying something about it, or supporting SSWUG, does not mean they know about it at all, never mind approve). Shouldn't they have the opportunity to learn about this practice? That was kind of the point of my posting this in the first place – and obviously to let them comment on either side of the argument; I'm not moderating anything here. I guess your suggestion is that I should just shut up and let it happen, and continue to let people be duped into buying a SSWUG subscription so that they can then be linked here and read my content for free?
Hi Aaron,
I feel your pain, but let us hear both sides in this dispute. Quite a few people speak at sswugs virtual conference:
http://www.vconferenceonline.com/shows/spring10/uvc/speakers.asp
including those whom we all know, such as Paul Nielsen, Kevin Kline, and Glenn Berry. Also Microsoft awards him the MVP award every year. Apparently some people approve of the business practices you are speaking about. What do you think?
The way around this thing happening is to be below-average like me and no one wants to republish your stuff 🙂 OK, maybe that's bad career advice.
Still, unforgivable…
Yikes. That's nasty. You're right to call them on it.
A summary of one of the many reason's I don't participate in SSWUG :-). Not knowingly, anyway…
Aaron, I agree with you completely. Referring some good content is okay, but not in a manner where you are placing it in the midst of hunderd adverts and on the top of it, it's shown confusingly as if you own the content.
Also I have seen blogs (dont intend to name anyone) where people say that default reference is BOL but example is provided by author. I completely fail to digest this concept, as 90% of their articles are rehashes of MSDN. This is just my personal opinion, but I see it more often on SQL/DBA based blogs than BI (SSIS/SSAS/SSRS) based blogs where one finds less value addition and more MSDN rehashing.
Aaron, I know what you mean. That's because all these guys want is 'da cash'. Contrarywise, when I created Codebix.com, I wanted to make an honest website that actually was meant to bring good content to prorgrammers (I was getting tired of my Google-Reader's capabilities).
So here's a content aggregator for you that's honest — http://codebix.com. Do have a look and give me your views on it. If there's anything you don't like tell me, we like to improve.
Your personal page on codebix.com is: http://codebix.com/blogs/blog/1183
Cheers!
Cyril Gupta
Well, I'd like to protest about McSQL comparing goats with those people at 'SSWUG'. Goats are fine and useful creatures that are an essential ingredient to curried goat. They may smell a bit but they don't engage in this sort of practice. I'd be very happy for Stephen Wynkoop and his 'SSWUG' merely to link to the 23 'Phil Factor' articles he does, even as a premium service to his subscribers. However, it should not be in such a way that can mislead people into believing that they are internal SSWUG articles on his site that they need a subscription to read, rather than a link to freely-available content on another site. He's certainly never asked my permission to do so.
Aaron, your logic is sound and you're right in pointing the finger.
The approach being used isn't honest as it tries to imply certain things that aren't true.
I agree with you. It's not illegal but I think it crosses an ethical line that I do not like to cross. I hae complained before and had my content removed. Someone from an Oracle site made the same note as you a few years ago and threatened to sue if his content was not removed
Aaron,
This is one thing we definitely agree on. I get the SSWUG newsletter, but just skim it. I refuse to join because of exactly what you have shared. Almost every article I have wanted to read on that site I have found for free somewhere else.
This is egregious aggregation, even for Scum Sucking Worthless Usurping Goats
Aaron, you're right on target with your criticism. If a website (especially one that charges for membership) wants to publish links to my blog posts or other content, I'm all for it – as long as it's not represented as being part of the members-only content section. This is not exactly plagarism, but it's not an honorable way to run a business either.
Sound logic, Aaron. Yes, you got it right. I agree.
That's a picture of Steve, right… not Eric?
And I think we've all been bitten this way. I prefer the way that the Database Weekly emails come out, with links directly to the original articles (not diverting through any other site).
I agree with you Aaron, 100%. I have also been bitten in the same way.